Bạn đang học về phương trình tan của đồ thị hàm số tại một điểm? Bạn có muốn biết cách viết phương trình này một cách chính xác và hiệu quả không? Hãy cùng tìm hiểu trong bài viết này!
Phương trình tiếp tuyến là gì?
Trong hình học, tiếp tuyến của đường cong tại một điểm là đường thẳng “chạm” vào đường cong tại điểm đó. Tiếp tuyến có thể được coi là đường thẳng “gần nhất” với đường cong tại điểm tiếp xúc.
Ý nghĩa của phương trình tiếp tuyến
Phương trình tiếp tuyến của đồ thị hàm số tại một điểm cho phép chúng ta tính toán độ dốc (độ dốc) của tiếp tuyến tại điểm đó. Độ dốc này cung cấp thông tin về tốc độ thay đổi của hàm số tại điểm tiếp tuyến.
Cách Viết Phương Trình Đường Tiếp Tuyến Của Đồ Thị Hàm Số Tại Một Điểm
Để viết phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm x0, ta thực hiện các bước sau:
- Tính đạo hàm f'(x) của hàm số.
- Tính giá trị của đạo hàm tại điểm x0, tức là f'(x0). Giá trị này là độ dốc của đường tiếp tuyến.
- Tìm tọa độ y0 của điểm tiếp xúc bằng cách thay x0 vào hàm f(x).
- Áp dụng công thức phương trình tiếp tuyến:
y – y0 = f'(x0)(x – x0)
Ví dụ minh họa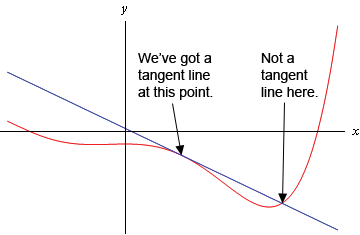
Ví dụ: Viết phương trình tiếp tuyến của đồ thị hàm số y = x² tại điểm có x0 = 1.
Giải pháp:
- Đạo hàm: f'(x) = 2x
- Tính độ dốc: f'(1) = 2
- Tính tọa độ: f(1) = 1² = 1
- Viết phương trình tiếp tuyến: y – 1 = 2(x – 1) => y = 2x – 1
Vậy phương trình tiếp tuyến của đồ thị hàm số y = x² tại điểm có x0 = 1 là y = 2x – 1.
Những câu hỏi thường gặp
Ứng dụng thực tế của phương trình tiếp tuyến là gì?
- Phương trình tiếp tuyến được sử dụng rộng rãi trong nhiều lĩnh vực như vật lý, kinh tế, kỹ thuật… để tính toán tốc độ thay đổi, tối ưu hóa, dự đoán xu hướng…
Có cách nào khác để tìm phương trình tiếp tuyến không?
- Ngoài việc sử dụng đạo hàm, chúng ta cũng có thể tìm phương trình tiếp tuyến bằng cách sử dụng giới hạn, công thức tính đường thẳng đi qua hai điểm…
Làm thế nào để kiểm tra xem phương trình tiếp tuyến có được viết đúng không?
- Bạn có thể kiểm tra điều này bằng cách vẽ đồ thị hàm số và đường tiếp tuyến trên cùng một hệ tọa độ. Nếu đường tiếp tuyến chỉ “chạm” vào đồ thị tại một điểm và có độ dốc khớp với giá trị tính toán, thì phương trình đường tiếp tuyến là đúng.
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về phương trình tiếp tuyến của đồ thị hàm số tại một điểm và cách viết phương trình này một cách chính xác. Nếu bạn có bất kỳ câu hỏi nào khác, đừng ngần ngại để lại bình luận bên dưới!
Mọi thắc mắc vui lòng gửi về Hotline 09633458xxx hoặc địa chỉ email [email protected] để làm rõ. Trân trọng!
Tuyên bố miễn trừ trách nhiệm: sesua.vn là website tổng hợp kiến thức từ nhiều nguồn,Vui lòng gửi email cho chúng tôi nếu có bất cứ vi phạm bản quyền nào! Xin cám ơn!
