Trong nhiều lĩnh vực như toán học, vật lý, kỹ thuật và khoa học, tính toán khoảng cách từ một điểm đến một đường thẳng là một kỹ năng cơ bản và quan trọng. Nó được sử dụng rộng rãi trong nhiều ứng dụng như phân tích không gian, thiết kế kỹ thuật, tối ưu hóa và lập trình. Trong bài viết này, chúng tôi sẽ đi sâu vào từng bước, cung cấp hướng dẫn chi tiết về cách tính khoảng cách từ một điểm đến một đường thẳng.
Cách tính khoảng cách giữa một điểm và một đường thẳng
Để tính khoảng cách từ một điểm đến một đường thẳng, chúng ta cần xác định các yếu tố liên quan như tọa độ của điểm và phương trình của đường thẳng. Khoảng cách này được định nghĩa là khoảng cách ngắn nhất từ điểm đến đường thẳng.
Xác định tọa độ của điểm
Một điểm được xác định bởi tọa độ của nó trong hệ tọa độ Descartes. Điểm có thể nằm trong mặt phẳng hai chiều (x, y) hoặc trong không gian ba chiều (x, y, z). Tùy thuộc vào số chiều, chúng ta sẽ sử dụng các công thức khác nhau để tính khoảng cách.
Tìm phương trình của đường thẳng
Một đường thẳng có thể được biểu diễn theo nhiều cách, chẳng hạn như phương trình tổng quát của một đường thẳng, phương trình của một đường thẳng qua hai điểm hoặc phương trình tham số của một đường thẳng. Chúng ta cần xác định dạng phương trình của một đường thẳng để áp dụng công thức khoảng cách chính xác.
Áp dụng công thức khoảng cách
Dựa trên tọa độ của một điểm và phương trình của một đường thẳng, chúng ta có thể áp dụng các công thức toán học để tính khoảng cách từ một điểm đến một đường thẳng. Các công thức này thay đổi tùy thuộc vào kích thước và hình dạng của phương trình đường thẳng.
Hướng dẫn từng bước để tính khoảng cách từ điểm đến đường thẳng
Để tính khoảng cách từ một điểm đến một đường thẳng, chúng ta sẽ làm theo các bước sau:
Bước 1: Xác định tọa độ của điểm
Đầu tiên, chúng ta cần biết tọa độ của điểm trong hệ tọa độ Descartes. Điểm có thể nằm trong mặt phẳng hai chiều (x, y) hoặc trong không gian ba chiều (x, y, z).
Bước 2: Xác định phương trình của đường thẳng
Tiếp theo, chúng ta cần xác định phương trình của đường thẳng. Một đường thẳng có thể được biểu diễn theo nhiều cách, chẳng hạn như phương trình tổng quát của một đường thẳng, phương trình của một đường thẳng qua hai điểm hoặc phương trình tham số của một đường thẳng.
Bước 3: Áp dụng công thức tính khoảng cách
Dựa trên tọa độ của điểm và phương trình của đường thẳng, chúng ta sẽ áp dụng công thức toán học thích hợp để tính khoảng cách từ điểm đến đường thẳng. Các công thức này thay đổi tùy thuộc vào kích thước và dạng của phương trình đường thẳng.
Bước 4: Tính toán kết quả
Thực hiện các phép tính cần thiết dựa trên công thức đã chọn và chúng ta sẽ nhận được kết quả là khoảng cách từ điểm đến đường thẳng.
Bước 5: Kiểm tra và đánh giá kết quả
Cuối cùng, chúng ta cần kiểm tra kết quả để đảm bảo tính chính xác và hợp lý. Nếu cần, chúng ta có thể thực hiện tính toán lại hoặc so sánh với các phương pháp khác để đảm bảo tính chính xác.
Bằng cách thực hiện theo các bước này, chúng ta sẽ có thể tính toán khoảng cách từ một điểm đến một đường thẳng một cách chính xác và hiệu quả.
Phương pháp chi tiết để xác định khoảng cách từ một điểm đến một đường thẳng
Khi tính khoảng cách từ một điểm đến một đường thẳng, chúng ta cần xem xét các trường hợp khác nhau dựa trên kích thước và hình dạng của phương trình đường thẳng. Sau đây là các phương pháp chi tiết cho từng trường hợp:
Tính khoảng cách từ một điểm đến một đường thẳng trong mặt phẳng hai chiều
Trên mặt phẳng hai chiều (x, y), chúng ta có thể sử dụng công thức sau để tính khoảng cách từ một điểm đến một đường thẳng:
Khoảng cách = |Ax + By + C| / √(A^2 + B^2)
Trong đó:
- (x, y) là tọa độ của điểm
- Ax + By + C = 0 là phương trình của đường thẳng.
- A, B, C là các hệ số của phương trình đường thẳng.
Chúng ta cần xác định các thông số này trước khi thực hiện tính toán.
Tính khoảng cách từ một điểm đến một đường thẳng trong không gian ba chiều
Trong không gian ba chiều (x, y, z), chúng ta có thể sử dụng công thức sau để tính khoảng cách từ một điểm đến một đường thẳng:
Khoảng cách = |Ax + By + Cz + D| / √(A^2 + B^2 + C^2)
Trong đó:
- (x, y, z) là tọa độ của điểm
- Ax + By + Cz + D = 0 là phương trình của đường thẳng
- A, B, C, D là các hệ số của phương trình đường thẳng.
Tương tự như trường hợp hai chiều, chúng ta cần xác định các tham số này trước khi thực hiện tính toán.
Tính khoảng cách từ một điểm đến một đường thẳng đi qua hai điểm
Nếu một đường thẳng được biểu diễn bởi hai điểm (x1, y1) và (x2, y2), chúng ta có thể sử dụng công thức sau:
Khoảng cách = |(y2 – y1)x – (x2 – x1)y + (x2y1 – x1y2)| / √((y2 – y1)^2 + (x2 – x1)^2)
Trong đó:
- (x, y) là tọa độ của điểm
- (x1, y1) và (x2, y2) là tọa độ của hai điểm xác định đường thẳng
Công thức này có thể áp dụng cho cả mặt phẳng hai chiều và không gian ba chiều.
Tính khoảng cách từ một điểm đến một đường thẳng theo dạng tham số
Nếu đường thẳng được biểu diễn dưới dạng tham số, chúng ta có thể sử dụng công thức sau:
Khoảng cách = |a(x0 – x) + b(y0 – y) + c(z0 – z)| / √(a^2 + b^2 + c^2)
Trong đó:
- (x, y, z) là tọa độ của điểm
- (x0, y0, z0) là một điểm trên đường thẳng
- a, b, c là các hệ số của phương trình tham số của đường thẳng.
Công thức này có thể áp dụng cho cả mặt phẳng hai chiều và không gian ba chiều.
Bằng cách áp dụng các công thức trên, chúng ta có thể tính toán khoảng cách từ một điểm đến một đường thẳng một cách chính xác và hiệu quả.
Thuật toán hiệu quả để tính khoảng cách từ điểm đến đường thẳng
Để tính khoảng cách từ một điểm đến một đường thẳng một cách hiệu quả, chúng ta có thể sử dụng một thuật toán cụ thể. Sau đây là một ví dụ về một thuật toán hiệu quả:
Thuật toán tính khoảng cách từ điểm đến đường thẳng
- Xác định tọa độ của điểm (x, y) hoặc (x, y, z).
- Xác định dạng phương trình đường thẳng (dạng tổng quát, qua hai điểm, dạng tham số).
- Nếu đường thẳng có phương trình dạng Ax + By + C = 0 hoặc Ax + By + Cz + D = 0:
- Tính giá trị của biểu thức Ax + By + C hoặc Ax + By + Cz + D.
- Tính giá trị căn bậc hai của A^2 + B^2 hoặc A^2 + B^2 + C^2.
- Khoảng cách = |Ax + By + C| / √(A^2 + B^2) hoặc |Ax + By + Cz + D| / √(A^2 + B^2 + C^2).
- Nếu một đường thẳng được xác định bởi hai điểm (x1, y1) và (x2, y2):
- Tính giá trị của biểu thức (y2 – y1)x – (x2 – x1)y + (x2y1 – x1y2).
- Tính giá trị căn bậc hai của (y2 – y1)^2 + (x2 – x1)^2.
- Khoảng cách = |(y2 – y1)x – (x2 – x1)y + (x2y1 – x1y2)| / √((y2 – y1)^2 + (x2 – x1)^2).
- Nếu đường thẳng được biểu diễn dưới dạng tham số:
- Tính giá trị của biểu thức a(x0 – x) + b(y0 – y) + c(z0 – z).
- Tính giá trị căn bậc hai của a^2 + b^2 + c^2.
- Khoảng cách = |a(x0 – x) + b(y0 – y) + c(z0 – z)| / √(a^2 + b^2 + c^2).
- Trả về khoảng cách từ điểm đến đường thẳng.
Bằng cách sử dụng thuật toán này, chúng ta có thể tính toán khoảng cách từ một điểm đến một đường thẳng một cách có hệ thống và hiệu quả. Nó giúp chúng ta xử lý các trường hợp khác nhau một cách rõ ràng và chính xác.
Công thức hữu ích để tính khoảng cách từ một điểm đến một đường thẳng
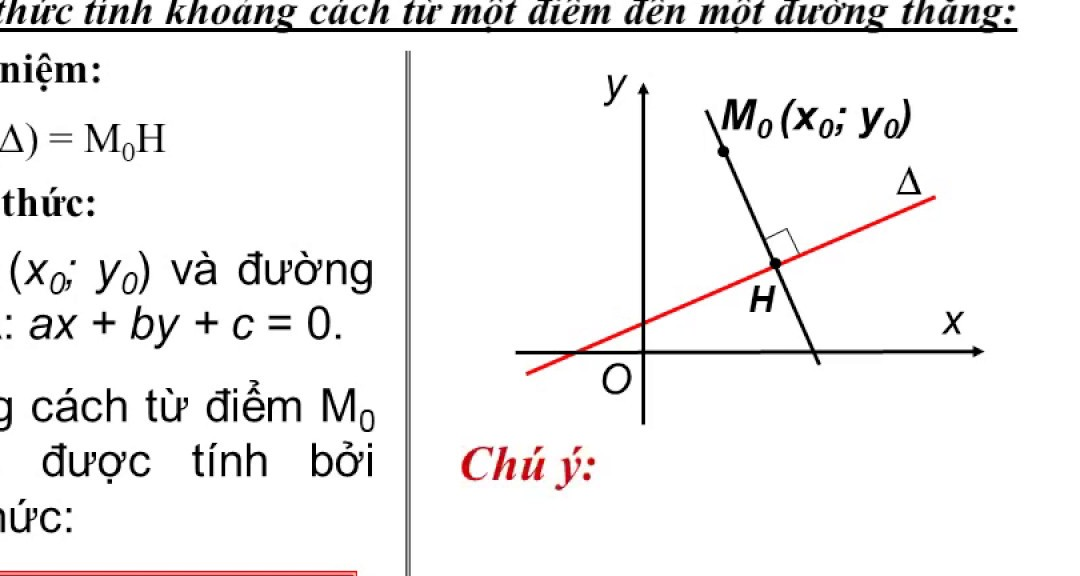
Trong phần này, chúng tôi sẽ tóm tắt các công thức hữu ích để tính khoảng cách từ một điểm đến một đường thẳng:
Công thức tính khoảng cách trong mặt phẳng hai chiều
Khoảng cách = |Ax + By + C| / √(A^2 + B^2)
Trong đó:
- (x, y) là tọa độ của điểm
- Ax + By + C = 0 là phương trình của đường thẳng.
- A, B, C là các hệ số của phương trình đường thẳng.
Công thức tính khoảng cách trong không gian ba chiều
Khoảng cách = |Ax + By + Cz + D| / √(A^2 + B^2 + C^2)
Trong đó:
- (x, y, z) là tọa độ của điểm
- Ax + By + Cz + D = 0 là phương trình của đường thẳng
- A, B, C, D là các hệ số của phương trình đường thẳng.
Công thức tính khoảng cách từ một điểm đến một đường thẳng đi qua hai điểm
Khoảng cách = |(y2 – y1)x – (x2 – x1)y + (x2y1 – x1y2)| / √((y2 – y1)^2 + (x2 – x1)^2)
Trong đó:
- (x, y) là tọa độ của điểm
- (x1, y1) và (x2, y2) là tọa độ của hai điểm trên đường thẳng
Công thức tính khoảng cách từ một điểm đến một đường thẳng dưới dạng tham số
Khoảng cách = |a(x0 – x) + b(y0 – y) + c(z0 – z)| / √(a^2 + b^2 + c^2)
Trong đó:
- (x, y, z) là tọa độ của điểm
- (x0, y0, z0) là một điểm trên đường thẳng
- a, b, c là các hệ số của phương trình tham số của đường thẳng.
Bằng cách sử dụng các công thức trên, chúng ta có thể dễ dàng tính khoảng cách từ một điểm đến một đường thẳng trong không gian hai chiều và ba chiều.
Ví dụ minh họa về quy trình tính khoảng cách từ một điểm đến một đường thẳng
Để minh họa quá trình tính khoảng cách từ một điểm đến một đường thẳng, hãy xem xét ví dụ sau:
Giả sử chúng ta có một điểm A có tọa độ (2, 3) và một đường thẳng được biểu diễn bằng phương trình x + y – 5 = 0 trên mặt phẳng hai chiều. Chúng ta muốn tính khoảng cách từ điểm A đến đường thẳng này.
Theo công thức trên, ta có:
- A(x, y) = (2, 3)
- Đường thẳng: x + y – 5 = 0
Áp dụng công thức tính khoảng cách từ một điểm đến một đường thẳng trong mặt phẳng hai chiều, ta có: Khoảng cách = |2 + 3 – 5| / √(1^2 + 1^2) Khoảng cách = |0| / √2 Khoảng cách = 0
Vậy khoảng cách từ điểm A đến đường thẳng x + y – 5 = 0 là 0. Điều này chứng tỏ điểm A nằm trên đường thẳng đã cho.
Qua ví dụ trên, chúng ta có thể thấy cách áp dụng công thức tính khoảng cách từ một điểm đến một đường thẳng một cách cụ thể và dễ hiểu.
Ứng dụng công thức tính khoảng cách từ một điểm đến một đường thẳng
Công thức tính khoảng cách từ một điểm đến một đường thẳng có nhiều ứng dụng trong đời sống thực tế và trong toán học. Sau đây là một số ứng dụng phổ biến của công thức này:
Trong hình học
- Xác định vị trí tương đối giữa một điểm và một đường thẳng.
- Tính khoảng cách an toàn khi lái xe trên đường.
- Các vấn đề thiết kế về tọa độ trong không gian.
Trong vật lý
- Xác định quỹ đạo của một vật chuyển động theo đường thẳng.
- Tính toán quỹ đạo của sóng ánh sáng hoặc sóng âm khi chúng chạm vào một bề mặt phẳng.
Trong học máy và xử lý hình ảnh
- Phân loại các đối tượng dựa trên khoảng cách đến đường thẳng gần nhất.
- Xác định vùng quan tâm trong hình ảnh dựa trên khoảng cách từ một điểm đến một đường thẳng.
Công thức tính khoảng cách từ một điểm đến một đường thẳng không chỉ giúp chúng ta hiểu được vị trí tương đối giữa các vật thể mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau.
Những lưu ý quan trọng cần nhớ khi tính khoảng cách từ một điểm đến một đường thẳng
Khi tính khoảng cách từ một điểm đến một đường thẳng, có một số lưu ý quan trọng mà chúng ta cần nhớ:
- Xác định rõ hệ số và tọa độ: Để áp dụng công thức tính khoảng cách, ta cần xác định chính xác hệ số và tọa độ của đường thẳng cũng như tọa độ của điểm.
- Kiểm tra lại phương trình: Trước khi tính toán, hãy kiểm tra lại phương trình của đường thẳng để tránh sai sót.
- Chú ý đến hướng của vectơ: Khi tính khoảng cách từ một điểm đến một đường thẳng, hãy chú ý đến hướng của vectơ và dấu của kết quả để đảm bảo độ chính xác.
- Sử dụng công thức thích hợp: Tùy thuộc vào cách biểu diễn đường thẳng, chúng ta cần chọn công thức tính khoảng cách thích hợp để đảm bảo tính toán chính xác.
Những lưu ý trên sẽ giúp chúng ta tính toán khoảng cách từ một điểm đến một đường thẳng một cách chính xác và hiệu quả.
Kết luận
Trong bài viết này, chúng ta đã tìm hiểu về cách tính khoảng cách từ một điểm đến một đường thẳng một cách chi tiết và cụ thể. Từ việc xác định công thức đến việc áp dụng thuật toán tính khoảng cách, chúng ta đã thấy rằng quá trình này đòi hỏi sự chính xác và logic.
Bằng cách áp dụng các công thức và thuật toán được trình bày, chúng ta có thể dễ dàng xác định khoảng cách từ một điểm đến một đường thẳng trong không gian hai chiều và ba chiều. Hiểu cách tính khoảng cách này không chỉ giúp chúng ta giải quyết các bài toán hình học mà còn mở ra nhiều ứng dụng thú vị trong cuộc sống thực và các lĩnh vực khoa học khác.
Mọi thắc mắc vui lòng gửi về Hotline 09633458xxx hoặc địa chỉ email [email protected] để làm rõ. Trân trọng!
Tuyên bố miễn trừ trách nhiệm: sesua.vn là website tổng hợp kiến thức từ nhiều nguồn,Vui lòng gửi email cho chúng tôi nếu có bất cứ vi phạm bản quyền nào! Xin cám ơn!














