Đường trung trực là gì? Tính chất và bài tập về đường trung trực

In plane geometry, perpendicular bisector is an important concept and is often used to solve many problems. Perpendicular bisector not only has special properties but also has many practical applications. In this article, we will learn in detail about perpendicular bisector, including definition, properties, drawing, equation, theorem, proof, exercises, applications and special points related to it.

What is a perpendicular bisector?

The perpendicular bisector of a line segment is the line that is perpendicular to the line segment and passes through the midpoint of the line segment. In other words, the perpendicular bisector divides the line segment into two equal parts.

Some characteristics of perpendicular bisector:

• The perpendicular bisector is perpendicular to a line segment.
• The perpendicular bisector passes through the midpoint of a line segment.
• The perpendicular bisector divides a line segment into two equal parts.

Examples of perpendicular bisector

Suppose we have a line segment AB, with A(x1, y1) and B(x2, y2). To draw the perpendicular bisector of line segment AB, we can:

1. Find the midpoint M of line segment AB.
2. Draw a line perpendicular to line segment AB and passing through point M.

The line just drawn is the perpendicular bisector of line segment AB.

Properties of perpendicular bisector

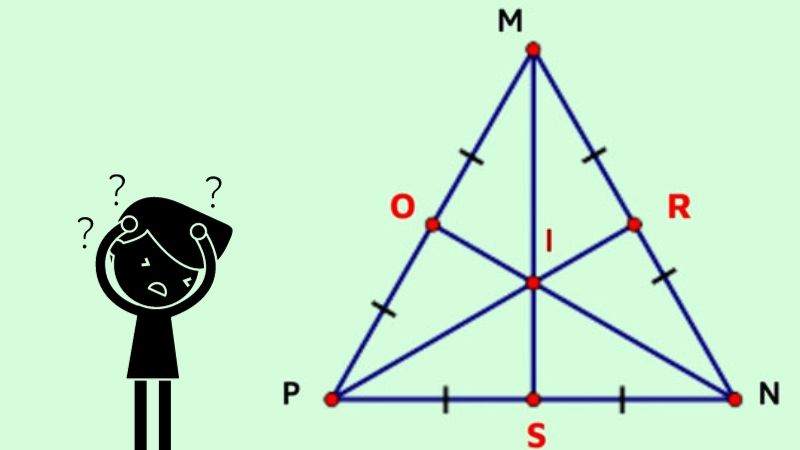
The perpendicular bisector has many special properties, here are some important properties:

1. The perpendicular bisector divides a line segment into two equal parts.

As mentioned above, the perpendicular bisector passes through the midpoint of a line segment, thus it divides the line segment into two equal parts.

2. The perpendicular bisector is perpendicular to a line segment.

A perpendicular bisector is always perpendicular to the line segment it bisects. This is because of the definition of a perpendicular bisector, when defining a perpendicular bisector, we must draw a line perpendicular to that line segment.

3. All points on the perpendicular bisector are equidistant from the two endpoints of the line segment.

Because the perpendicular bisector divides a line segment into two equal parts, all points on the perpendicular bisector are equidistant from the two endpoints of the line segment.

4. The perpendicular bisector of a line segment is the average of the two endpoints of that line segment.

The midpoint of a line segment is calculated using the formula: $M = \left(\frac\right)$

Because the perpendicular bisector passes through the midpoint of the line segment, the perpendicular bisector is the average of the two endpoints of the line segment.

5. The perpendicular bisector of a line segment is the set of all points equidistant from the two endpoints of that line segment.

As mentioned above, all points on the perpendicular bisector are equidistant from the two endpoints of the line segment. Therefore, the perpendicular bisector is the set of all points equidistant from the two endpoints of the line segment.

Exercises on perpendicular bisector

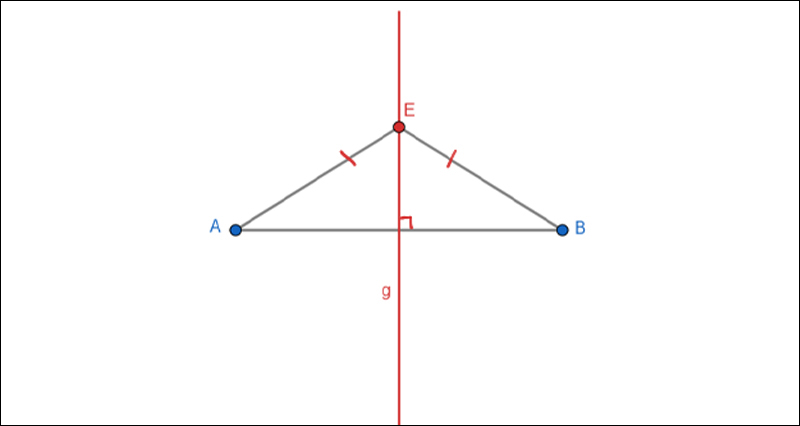
After learning about the definition and properties of perpendicular bisector, we will look at some exercises related to perpendicular bisector.

Exercise 1: Draw the perpendicular bisector of a line segment

Request: Draw the perpendicular bisector of line segment AB, with A(x1, y1) and B(x2, y2).

Prize:

1. Find the midpoint M of line segment AB: $M = \left(\frac\right)$
2. Draw a line perpendicular to line segment AB and passing through point M. The line just drawn is the perpendicular bisector of line segment AB.

Exercise 2: Find the equation of the perpendicular bisector of a line segment

Request: Find the equation of the perpendicular bisector of line segment AB, with A(x1, y1) and B(x2, y2).

Prize:

1. Find the midpoint M of line segment AB: $M = \left(\frac\right)$
2. Find the slope of line AB: $k = \frac$
3. Find the slope of the perpendicular bisector: Since the perpendicular bisector is perpendicular to line segment AB, the slope of the perpendicular bisector is $k’ = -\frac$.
4. Find the equation of the perpendicular bisector: The equation of the perpendicular bisector has the form: $y – y_M = k'(x – x_M)$ Substituting the values ​​found, we have: $y – \frac)$ After simplifying, we have the equation of the perpendicular bisector: $y = -\frac$

Exercise 3: Prove that three points are collinear

Request: Prove that three points A(x1, y1), B(x2, y2) and C(x3, y3) are collinear if and only if the perpendicular bisector of AB and the perpendicular bisector of AC coincide.

Prize:

1. Suppose three points A, B, C are collinear.
   • The perpendicular bisectors of AB and AC are both perpendicular to line segments AB and AC.
   • Since the three points are collinear, the midpoints of AB and AC coincide.
   • Therefore, the perpendicular bisectors of AB and AC coincide.
2. Suppose the perpendicular bisectors of AB and AC coincide.
   • The midpoints of AB and AC coincide.
   • Since the three points lie on the perpendicular bisector, they are collinear.

Thus, three points A, B, C are collinear if and only if the perpendicular bisector of AB and the perpendicular bisector of AC coincide.

How to draw a perpendicular bisector of a line segment

To draw the perpendicular bisector of a line segment, we can use one of the following methods:

Method 1: Using a compass and ruler

1. Mark two points A and B on the plane.
2. Use a compass to measure the distance from A to B.
3. Keeping the compass distance the same, place one foot of the compass on point A and draw an arc. Do the same with point B.
4. The line passing through the intersection of two arcs is the perpendicular bisector of line segment AB.

Method 2: Using Equations

1. Find the coordinates of the midpoint M of line segment AB. $M = \left(\frac\right)$
2. Find the slope of line AB. $k = \frac$
3. Find the slope of the perpendicular bisector, since it is perpendicular to AB. $k’ = -\frac$
4. Write the equation of the perpendicular bisector: $y – y_M = k'(x – x_M)$

Thus, by finding the coordinates of the midpoint and the slope of the perpendicular bisector, we can write down the equation of the perpendicular bisector.

Equation of perpendicular bisector of line segment

As presented above, the equation of the perpendicular bisector of a line segment AB has the form:

$y – y_M = k'(x – x_M)$

In there:

• (xM, yM) are the coordinates of the midpoint of line segment AB.
• k’ is the slope of the perpendicular bisector, calculated as $k’ = -\frac$.
• Write the equation of the perpendicular bisector in the form $y – y_M = k'(x – x_M)$.

For example: Find the equation of the perpendicular bisector of line segment AB, with A(1, 2) and B(4, 5).

Prize:

• 1. Find the coordinates of the midpoint M of line segment AB: $M = \left(\frac\right) = (2.5, 3.5)$
  2. Calculate the slope coefficient k of line segment AB: $k = \frac = 1$
  3. Calculate the slope k’ of the perpendicular bisector: $k’ = -\frac = -1$
  4. Write the equation of the perpendicular bisector: $y – 3.5 = -1(x – 2.5)$ Simplifying, we have: $y = -x + 6$

So the equation of the perpendicular bisector of line segment AB is $y = -x + 6$.

Theorem on perpendicular bisector

Theorem 1: Three points are collinear if and only if the perpendicular bisectors of two of the three line segments formed by the three points coincide.

Theorem 2: All points on the perpendicular bisector of a line segment are equidistant from the two endpoints of that line segment.

Theorem 3: The perpendicular bisector of a line segment is the set of all points equidistant from the two endpoints of that line segment.

Theorem 4: The perpendicular bisector of a line segment is always perpendicular to that line segment.

Theorem 5: The intersection point of two perpendicular bisectors of two different line segments is the midpoint of those two line segments.

How to prove three points are collinear

To prove that three points A(x1, y1), B(x2, y2) and C(x3, y3) are collinear, we can use the following method:

Step 1: Using geometry

• 1. Draw the perpendicular bisector of line segments AB and AC.
  2. If these two perpendicular bisectors coincide at a point D, then three points A, B, C are collinear.
  3. If the two perpendicular bisectors do not coincide, then the three points A, B, C are not collinear.

Step 2: Use the slope property

• 1. Calculate the slope coefficient k1 of line segment AB and the slope coefficient k2 of line segment AC.
  2. If k1 = k2, that means two line segments AB and AC are parallel, therefore three points A, B, C are collinear.
  3. If k1 ≠ k2, that means two line segments AB and AC intersect, therefore three points A, B, C are not collinear.

Thus, we can prove that three points are collinear by using the perpendicular bisector theorem and the slope property of a line segment.

Advanced exercises on perpendicular bisector

Exercise 1:

Given three points A(1, 2), B(3, 4) and C(5, 6). Prove that these three points are collinear using the perpendicular bisector.

Prize:

• • First, we calculate that the midpoint of line segment AB is M(2, 3).
  • The slope of line segment AB is k = 1.
  • The slope of the perpendicular bisector of AB is k’ = -1.
  • Write the equation of the perpendicular bisector of AB: $y – 3 = -1(x – 2)$, or $y = -x + 5$.
  • Similarly, we can calculate the equation of the perpendicular bisector of AC as $y = -x + 7$.
  • Because the two perpendicular bisectors coincide at point M(2, 3), the three points A, B, C are collinear.

Exercise 2:

Given three points A(-1, 2), B(2, 0) and C(4, -2). Prove that these three points are collinear using the slope property.

Prize:

• • The slope of line segment AB is k1 = -2/3.
  • The slope of line segment AC is k2 = -2/3.
  • Because k1 = k2, the three points A, B, C are collinear.

Through these advanced exercises, we can apply our knowledge of perpendicular bisectors to prove properties of three collinear points.

Applications of perpendicular bisector

Perpendicular bisector is not only a concept in geometry but also widely applied in practice. Here are some applications of perpendicular bisector:

1. In architecture

In architecture, determining the perpendicular bisector of a line segment helps in determining the position of columns, beams, or other constructions. This helps in making the construction accurate and uniform.

2. In technology

In technology, perpendicular bisector is used to determine the position of moving devices, sensors, or robots. Calculating perpendicular bisector helps improve the accuracy and performance of automated systems.

3. In GPS positioning

In the global positioning system (GPS), the principle of perpendicular bisector is applied to determine the exact location of points on a map. GPS devices calculate positions based on the perpendicular bisector of signals from satellites.

With such practical applications, the perpendicular bisector plays an important role in solving problems related to position and distance in space.

Special points regarding perpendicular bisector

1. Center point of triangle

In geometry, the center point of a triangle is the intersection of the three perpendicular bisectors of the sides of the triangle. This center point has many special and important properties in the study of triangles.

2. The perpendicular bisector of a line segment is perpendicular to the given line.

If we have a line segment and want to draw a perpendicular bisector of it such that the perpendicular bisector is perpendicular to another given line, we can use the slope property to solve this problem.

3. The perpendicular bisector of a line segment is parallel to a given line.

When we need to find the perpendicular bisector of a line segment so that it is parallel to a given line, we can also apply knowledge of slope coefficients to solve this problem.

These special points are closely related to the perpendicular bisector and can be applied in many complex geometric problems.

Conclude

In this article, we have learned about perpendicular bisector, from basic concepts to its properties, equations and applications. We have also become familiar with how to draw perpendicular bisector, prove three points are collinear and special points related to perpendicular bisector. Perpendicular bisector is not only a geometric concept but also has important practical applications, helping us better understand space and position in space. Hopefully this article will help you better understand perpendicular bisector and apply this knowledge to practice flexibly and effectively.

For any questions, please send to Hotline 09633458xxx or email address [email protected] for clarification. Best regards!