Diện tích tam giác: Công thức, cách tính và các dạng bài tập

Giới thiệu Hình tam giác là một hình phổ biến trong toán học, được xác định bởi ba cạnh và ba góc. Diện tích của một hình tam giác, biểu diễn diện tích bề mặt được bao quanh bởi các cạnh của hình tam giác, là một khái niệm quan trọng trong hình học. Bài viết này trình bày các công thức cơ bản, phương pháp tính toán và bài tập liên quan đến diện tích của một hình tam giác.

1. Công thức tính diện tích hình tam giác

Trong phần này, chúng ta sẽ khám phá các công thức khác nhau được sử dụng để tính diện tích của một hình tam giác, tùy thuộc vào thông tin đã biết về hình tam giác đó.

1.1. Sử dụng độ dài ba cạnh (công thức Heron)

$$S = \sqrt$$ trong đó:

• S là diện tích của tam giác
• a, b, c là độ dài ba cạnh của tam giác
• p là nửa chu vi của tam giác: p = (a + b + c) / 2

1.2. Sử dụng chiều cao và cơ sở

$$S = \frac bh$$ trong đó:

• S là diện tích của tam giác
• b là chiều dài của đáy
• h là chiều cao tương ứng với cạnh đáy

1.3. Sử dụng tích vô hướng của hai vectơ cạnh

$$S = \frac \Vert$$ trong đó:

• S là diện tích của tam giác
• AB, AC là hai vectơ hai bên của tam giác

2. Cách tính diện tích hình tam giác

Ngoài việc áp dụng trực tiếp các công thức đã cho, còn có một số cách khác để tính diện tích tam giác một cách hiệu quả.

2.1. Phân đôi tam giác

Chia một tam giác thành hai tam giác nhỏ hơn bằng cách vẽ một đường thẳng từ một đỉnh đến điểm giữa của cạnh đối diện.

2.2. Giải tam giác vuông

Nếu tam giác là tam giác vuông, hãy sử dụng định lý Pythagore hoặc tỉ số lượng giác để tìm chiều cao hoặc đáy.

2.3. Sử dụng lưới vuông

Đặt một lưới lên hình tam giác và đếm số ô vuông bên trong hình tam giác để ước tính diện tích.

3. Các loại bài tập về diện tích hình tam giác

3.1. Tính diện tích tam giác khi biết độ dài ba cạnh

Ví dụ: Tính diện tích hình tam giác có độ dài ba cạnh lần lượt là 5 cm, 6 cm và 8 cm.

3.2. Tìm đáy hoặc chiều cao khi biết diện tích và một cạnh.

Ví dụ: Một hình tam giác có diện tích 24 cm2 và chiều cao 6 cm. Tìm độ dài đáy.

3.3. Tính diện tích tam giác bằng vectơ

Ví dụ: Cho tam giác ABC có A(1, 2), B(3, 4), C(5, 1). Tính diện tích tam giác ABC bằng phép tính vectơ.

4. Diện tích tam giác cân và tam giác đều

4.1. Tam giác cân

• Tam giác cân có hai cạnh bằng nhau.
• Công thức tính diện tích tam giác cân: $$S = \frac bh$$ trong đó:
• b là chiều dài của đáy
• h là chiều cao từ đỉnh còn lại đến cạnh đáy

4.2. Tam giác đều

• Một tam giác đều có ba cạnh bằng nhau và ba góc bằng nhau.
• Công thức tính diện tích tam giác đều: $$S = \frac a^2$$ trong đó:
• a là độ dài một cạnh của tam giác đều

5. Diện tích các loại hình tam giác khác

5.1. Tam giác vuông

• Một tam giác vuông có một góc vuông (90 độ).
• Công thức tính diện tích tam giác vuông: $$S = \frac ab$$ trong đó:
• a, b là độ dài hai cạnh góc vuông

5.2. Tam giác tù

• Một tam giác tù có một góc tù (lớn hơn 90 độ).
• Không có công thức chung nào cho diện tích tam giác tù.

6. Diện tích một phần của hình tam giác

6.1. Đường phân giác của góc

• Đường phân giác của một góc chia tam giác thành hai tam giác nhỏ hơn.
• Diện tích của các tam giác nhỏ hơn tỉ lệ thuận với độ dài các cạnh tương ứng của chúng.

6.2. Đường trung bình động

• Đường trung bình của một cạnh thì song song với cạnh đó và bằng nửa độ dài cạnh đó.
• Diện tích tam giác tạo bởi đường trung tuyến bằng nửa diện tích tam giác ban đầu.

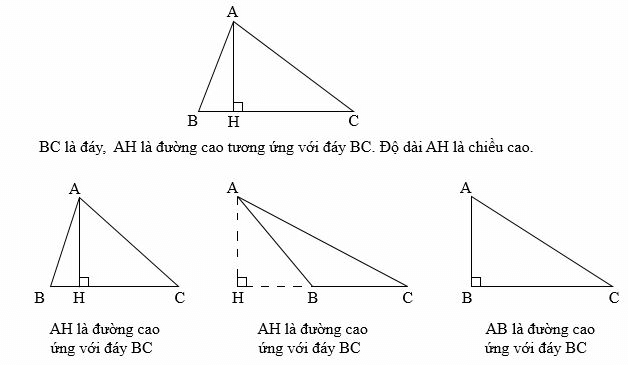
6.3 Chiều cao

• Đường cao của tam giác vuông góc với một cạnh và đi qua đỉnh đối diện.
• Diện tích hình tam giác nhỏ tạo bởi chiều cao bằng một nửa diện tích hình tam giác ban đầu.

Kết luận

Hiểu và áp dụng các công thức tính diện tích tam giác là điều cần thiết trong hình học. Bài viết này cung cấp nền tảng vững chắc để giải quyết nhiều loại bài toán liên quan đến diện tích tam giác, từ các trường hợp đơn giản đến phức tạp hơn.

Mọi thắc mắc vui lòng gửi về Hotline 09633458xxx hoặc địa chỉ email [email protected] để làm rõ. Trân trọng!