Hình thoi là một tứ giác đặc biệt có bốn cạnh bằng nhau và hai cặp cạnh đối diện song song với nhau. Diện tích của hình thoi được tính theo nhiều cách khác nhau tùy thuộc vào các thông số đã biết của hình thoi. Trong bài viết này, chúng ta sẽ tìm hiểu các công thức tính diện tích của hình thoi dựa trên các thông số khác nhau.
Công thức tính diện tích hình thoi
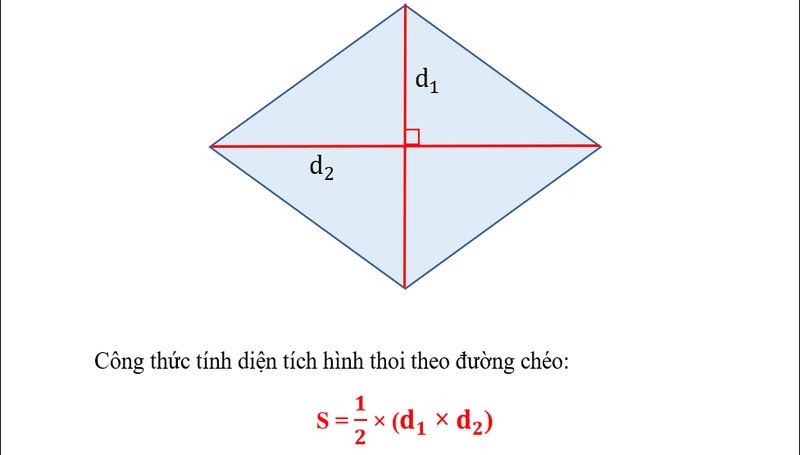
Công thức tổng quát
Công thức tổng quát để tính diện tích hình thoi theo độ dài hai đường chéo d₁ và d₂ là:
S = (d₁ x d₂) / 2
Trong đó:
- S là diện tích hình thoi (diện tích đơn vị)
- d₁ là độ dài đường chéo đầu tiên (độ dài đơn vị)
- d₂ là độ dài đường chéo thứ hai (độ dài đơn vị)
Ví dụ: Một hình thoi có đường chéo thứ nhất dài 10cm, đường chéo thứ hai dài 6cm. Diện tích của hình thoi là:
S = (10cm x 6cm) / 2 = 30cm²
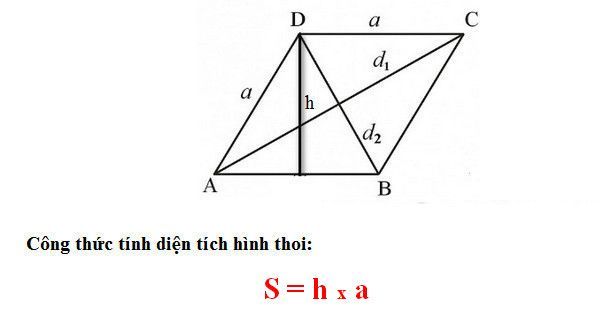
Công thức tính theo cạnh
Trường hợp ta biết độ dài một cạnh của hình thoi (ký hiệu là a) và chiều cao từ cạnh đó tới cạnh đối diện (ký hiệu là h) thì ta có thể tính được diện tích hình thoi theo công thức:
S = trục
Trong đó:
- S là diện tích hình thoi (diện tích đơn vị)
- a là độ dài một cạnh của hình thoi (đơn vị đo độ dài)
- h là chiều cao từ cạnh a đến cạnh đối diện (chiều dài đơn vị)
Ví dụ: Một hình thoi có cạnh bằng 5cm, chiều cao từ cạnh đó đến cạnh đối diện dài 3cm. Diện tích hình thoi là:
S = 5cm x 3cm = 15cm²
Công thức tính theo góc
Ngoài ra, diện tích hình thoi cũng có thể tính theo góc giữa hai đường chéo (ký hiệu là θ). Công thức tính diện tích hình thoi theo góc là:
S = (d₁ x d₂ x sin θ) / 2
Trong đó:
- S là diện tích hình thoi (diện tích đơn vị)
- d₁ là độ dài đường chéo đầu tiên (độ dài đơn vị)
- d₂ là độ dài đường chéo thứ hai (độ dài đơn vị)
- θ là góc giữa hai đường chéo (tính bằng độ)
Ví dụ: Một hình thoi có đường chéo thứ nhất dài 10cm, đường chéo thứ hai dài 6cm và góc giữa hai đường chéo bằng 60°. Diện tích hình thoi là:
S = (10 cm x 6 cm x sin60°) / 2 = 25,98 cm²
Một số công thức tính diện tích hình thoi khác
Ngoài những công thức chính nêu trên, còn có một số công thức khác để tính diện tích hình thoi như:
- Công thức tính diện tích hình thoi theo chu vi (ký hiệu là P) và độ dài đường chéo (ký hiệu là d):
S = P x d / 4
- Công thức tính diện tích hình thoi dựa vào độ dài bốn cạnh (ký hiệu là a₁, a₂, a₃ và a₄):
S = √((a₁ + a₃) x (a₂ + a₄)) – ((a₂ – a₄) x (a₃ – a₁)) / 4
- Công thức tính diện tích hình thoi theo bán kính đường tròn nội tiếp (ký hiệu là r):
S = 4 x r²
Ví dụ minh họa
Ví dụ 1: Tính diện tích hình thoi ABCD có hai đường chéo AC = 10 cm và BD = 6 cm.
Giải: Áp dụng công thức tính diện tích hình thoi theo đường chéo, ta có:
S = (AC x BD) / 2 = (10 cm x 6 cm) / 2 = 30 cm²
Ví dụ 2: Tính diện tích hình thoi MNPQ có cạnh MN = 5 cm và chiều cao từ đỉnh M đến cạnh NQ là 3 cm.
Giải: Áp dụng công thức tính diện tích hình thoi theo cạnh và chiều cao, ta có:
S = MN x MQ = 5cm x 3cm = 15cm²
Bảng tóm tắt công thức tính diện tích hình thoi
| Công thức | Mô tả |
|---|---|
| S = (d₁ x d₂) / 2 | Tính diện tích theo độ dài hai đường chéo |
| S = trục | Tính diện tích theo cạnh và chiều cao |
| S = (d₁ x d₂ x sin θ) / 2 | Tính diện tích dựa vào độ dài hai đường chéo và góc giữa hai đường chéo. |
| S = P x d / 4 | Tính diện tích theo chu vi và độ dài đường chéo |
| S = √((a₁ + a₃) x (a₂ + a₄)) – ((a₂ – a₄) x (a₃ – a₁)) / 4 | Tính diện tích theo độ dài bốn cạnh |
| S = 4 x r² | Tính diện tích theo bán kính của hình tròn nội tiếp |
Kết luận
Công thức diện tích hình thoi là công cụ hữu ích để tính diện tích hình thoi một cách chính xác. Tùy thuộc vào các thông số đã biết của hình thoi, có nhiều công thức khác nhau có thể được sử dụng để tính diện tích hình thoi. Việc hiểu các công thức này rất quan trọng để giải các bài toán hình thoi trong toán học và các lĩnh vực khác. Hy vọng bài viết này đã giúp bạn hiểu thêm về công thức diện tích hình thoi và cách áp dụng chúng vào các bài toán thực tế.
Mọi thắc mắc vui lòng gửi về Hotline 09633458xxx hoặc địa chỉ email [email protected] để làm rõ. Trân trọng!
Tuyên bố miễn trừ trách nhiệm: sesua.vn là website tổng hợp kiến thức từ nhiều nguồn,Vui lòng gửi email cho chúng tôi nếu có bất cứ vi phạm bản quyền nào! Xin cám ơn!
- Cách mở cốp xe Sh Mode khi bạn mất chìa nhanh nhất
- Phân tích bài thơ “Vội vàng” của Xuân Diệu – Tuyển chọn những bài phân tích hay nhất
- Giá ốc nhồi (ốc nhồi giống, thương phẩm) bao nhiêu tiền 1kg hiện nay?
- Cách vẽ xe tải đẹp đơn giản, nhìn như thật
- 20+ Cách vẽ lá cây đơn giản mà đẹp nhất cho bé học tập














