Đường tròn là một trong những hình học cơ bản và quan trọng trong toán học. Nó được sử dụng rộng rãi trong nhiều lĩnh vực như hình học, vật lý, kỹ thuật và thiết kế. Trong đường tròn, secant là một khái niệm quan trọng và đóng vai trò quan trọng trong việc xác định các tính chất của đường tròn. Trong bài viết này, chúng ta sẽ tìm hiểu về secant của đường tròn, cách xác định nó và các ứng dụng của nó.
Đường cắt của một đường tròn là gì?
Đường cắt của một đường tròn là đường thẳng đi qua tâm của đường tròn và cắt đường tròn tại hai điểm. Các điểm giao nhau này được gọi là điểm cắt. Đường cắt là một khái niệm quan trọng trong hình học và được sử dụng để xác định các tính chất của một đường tròn.
Cách xác định đường cắt của một đường tròn
Để xác định đường cắt của một đường tròn, chúng ta cần biết tâm và bán kính của đường tròn. Sau đó, chúng ta sẽ sử dụng công thức sau để tính:
- Điểm cắt 1: $P_1 = (x_1, y_1) = (a + r\cos$
Trong đó:
- $a$ và $b$ là tọa độ tâm của đường tròn
- $r$ là bán kính của hình tròn
- $d$ là đoạn thẳng nối hai giao điểm của đường cắt
- $d_1$ và $d_2$ là các đoạn thẳng nối một điểm giao nhau của đường cắt với tâm
- $d_3$ là đoạn thẳng nối giao điểm của đường cắt với bất kỳ điểm nào trên đường tròn.
Ứng dụng của phương pháp cắt
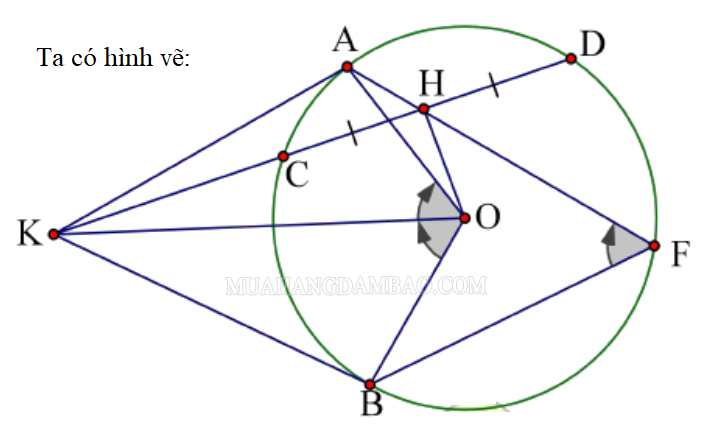
Phương pháp cắt có nhiều ứng dụng thực tế. Một số ứng dụng phổ biến của nó bao gồm:
Thiết kế hình tròn
Khi thiết kế hình tròn, các đường cắt được sử dụng để xác định các đặc tính của hình tròn như bán kính, tâm và phương trình của hình tròn. Điều này làm cho quá trình thiết kế dễ dàng và chính xác hơn.
Thiết kế bánh xe
Trong thiết kế bánh xe, đường cắt được sử dụng để xác định các đặc tính của bánh xe như bán kính và tâm. Điều này giúp sản xuất bánh xe dễ dàng và chính xác hơn.
Thiết kế đồ họa
Trong đồ họa máy tính, đường cắt được sử dụng để vẽ các đường tròn và các đường tròn liên quan. Phần mềm đồ họa thường sử dụng công thức cắt để tính các điểm trên một đường tròn và vẽ chúng trên màn hình.
Các bài toán liên quan đến đường cắt của đường tròn
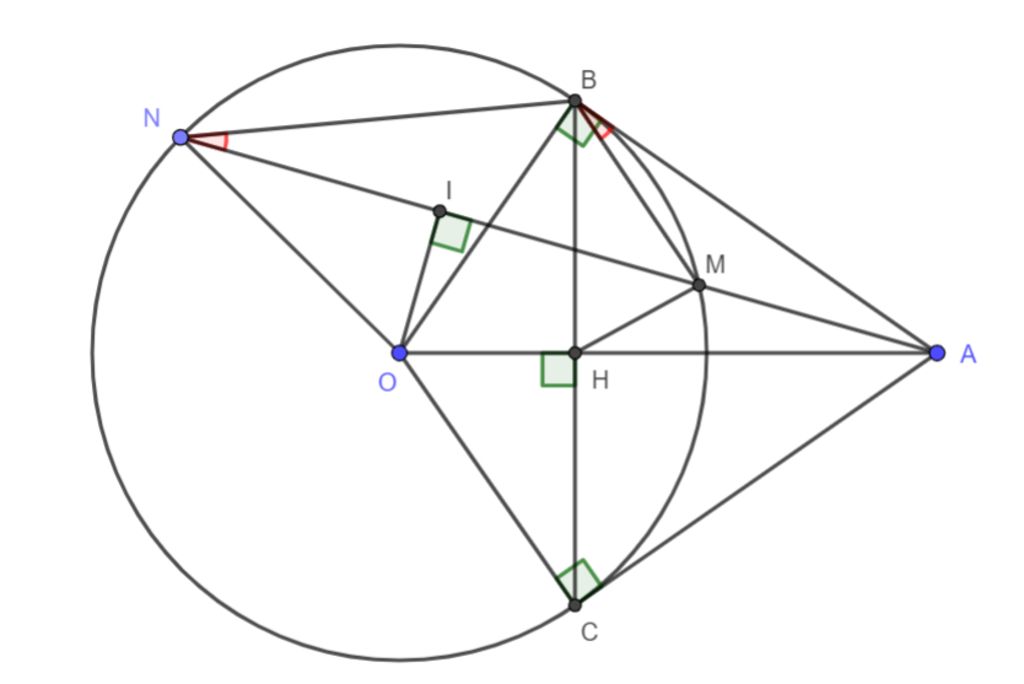
Đường cắt của đường tròn có nhiều ứng dụng thực tế và đã được sử dụng để giải quyết nhiều bài toán khó trong toán học. Một số bài toán liên quan đến đường cắt của đường tròn bao gồm:
Bài toán tìm tọa độ giao điểm của đường cắt
Bài toán này yêu cầu chúng ta tìm tọa độ hai giao điểm của đường cắt trên đường tròn. Để giải bài toán này, chúng ta có thể sử dụng công thức đã đề cập ở phần trước.
Bài toán tính diện tích cắt
Bài toán này yêu cầu chúng ta tính diện tích đường cắt trên hình tròn. Để giải bài toán này, chúng ta có thể sử dụng các công thức tính diện tích hình tròn và hình tam giác để tính diện tích đường cắt.
Bài toán tính khoảng cách giữa hai điểm cắt nhau của một đường thẳng cắt nhau
Bài toán này yêu cầu chúng ta tính khoảng cách giữa hai điểm cắt nhau của đường tròn. Để giải bài toán này, chúng ta có thể sử dụng công thức đã đề cập ở phần trước.
Tổng quan về các đường cắt
Đường cắt là một khái niệm quan trọng trong hình học và đóng vai trò quan trọng trong việc xác định tính chất của đường tròn. Nó có thể được sử dụng để giải quyết nhiều bài toán khó trong toán học và có nhiều ứng dụng thực tế. Chúng ta có thể sử dụng các công thức đã đề cập để tính các điểm trên đường cắt và giải các bài toán liên quan đến nó.
Kết luận về đường cắt
Trong bài viết này, chúng ta đã tìm hiểu về đường cắt của một đường tròn, cách xác định đường cắt và các loại đường cắt. Chúng ta cũng đã tìm hiểu về cấu trúc đường cắt và ứng dụng của nó trong thực tế. Cuối cùng, chúng ta đã tìm hiểu về một số bài toán liên quan đến đường cắt và khái quát của nó. Đường cắt là một khái niệm quan trọng và đóng vai trò quan trọng trong nhiều lĩnh vực khác nhau, và việc hiểu chúng sẽ giúp chúng ta áp dụng chúng vào thực tế và giải quyết các bài toán khó trong toán học.
Mọi thắc mắc vui lòng gửi về Hotline 09633458xxx hoặc địa chỉ email [email protected] để làm rõ. Trân trọng!
Tuyên bố miễn trừ trách nhiệm: sesua.vn là website tổng hợp kiến thức từ nhiều nguồn,Vui lòng gửi email cho chúng tôi nếu có bất cứ vi phạm bản quyền nào! Xin cám ơn!














