Cấp Số Cộng: Khái Niệm, Công Thức, Và Ứng Dụng

Cấp số cộng là một dãy số trong đó mỗi số hạng lớn hơn số hạng trước một lượng không đổi, gọi là hiệu chung. Dãy số này đóng vai trò quan trọng trong nhiều lĩnh vực toán học, bao gồm đại số, giải tích và thống kê. Trong bài viết này, chúng ta sẽ khám phá khái niệm về cấp số cộng, các công thức liên quan và ứng dụng của chúng trong nhiều ngữ cảnh khác nhau.

Công thức tính cộng

Công thức số hạng thứ n

Công thức quan trọng nhất liên quan đến cấp số cộng là công thức số hạng thứ n, được cho bởi:

an = a1 + (n – 1)d

• an: số hạng thứ n của cấp số cộng
• a1: số hạng đầu tiên của cấp số cộng
• n: thứ tự các số hạng trong cấp số cộng
• d: sai phân chung (lượng hằng số được thêm vào mỗi số hạng)

Công thức tính tổng n số hạng đầu tiên

Một công thức quan trọng khác là công thức tính tổng của n số hạng đầu tiên của một cấp số cộng, được cho bởi:

Sn = n/2(a1 + an)

• Sn: tổng n số hạng đầu tiên của cấp số cộng
• n: số từ cần thêm vào
• a1: số hạng đầu tiên của cấp số cộng
• an: số hạng thứ n của cấp số cộng

Các loại cấp số cộng

Tiến trình số học lũy tiến

Trong một cấp số cộng tăng dần, hiệu d là một số dương. Điều này có nghĩa là mỗi số hạng lớn hơn số hạng trước nó.

Giảm tiến trình phụ gia

Trong một cấp số cộng giảm dần, hiệu d là số âm. Điều này có nghĩa là mỗi số hạng nhỏ hơn số hạng trước nó.

Tiến độ bằng 0

Trong một cấp số cộng bằng 0, hiệu d là 0. Điều này có nghĩa là tất cả các số hạng trong cấp số cộng đều bằng nhau.

Ứng dụng của cấp số cộng

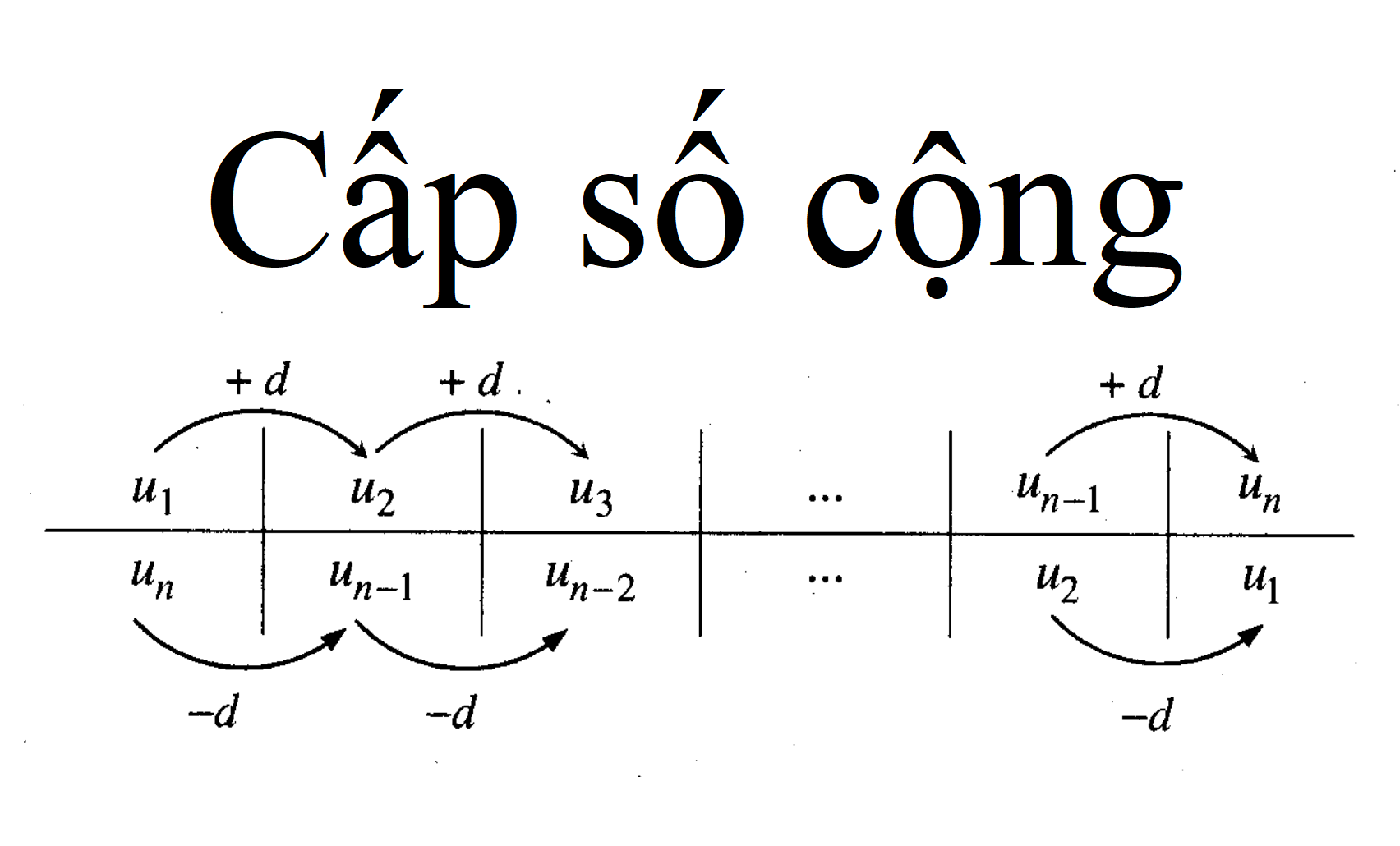
Giải quyết vấn đề về trình tự

Cấp số cộng thường được sử dụng để giải các bài toán liên quan đến dãy, chẳng hạn như tìm số hạng thứ n hoặc tổng của n số hạng đầu tiên.

Mô hình tăng trưởng hoặc suy thoái hiện tượng

Cấp số cộng có thể được sử dụng để mô hình hóa các hiện tượng tăng hoặc giảm với tốc độ không đổi. Ví dụ, trong mô hình tăng trưởng dân số, sự khác biệt chung thể hiện sự gia tăng dân số theo thời gian.

Cộng với đuôi

Khi cộng các số hạng liên tiếp của một cấp số cộng, chúng ta tạo ra một cấp số cộng mới. Quá trình này được gọi là phép cộng đuôi và có thể được sử dụng để tính tổng của nhiều cấp số cộng.

Sự kết hợp

Hai cấp số cộng có thể được kết hợp thành một cấp số cộng mới. Quá trình này được gọi là kết hợp số học và có thể được sử dụng để tạo ra các cấp số học mới với các thuộc tính mong muốn.

vi phân

Cấp số cộng có thể được sử dụng để lấy đạo hàm một hàm. Quá trình này liên quan đến việc tìm giới hạn thương của hai số hạng liền kề khi khoảng cách giữa các số hạng tiến tới 0.

Ví dụ về cấp số cộng

Ví dụ 1: Tiến trình số học lũy tiến

Cho một cấp số cộng có số hạng đầu tiên là 10 và hiệu chung là 5. Tìm tổng của 10 số hạng đầu tiên.

Phần thưởng:

Ví dụ 2: Giảm tiến trình phụ gia

Cho một cấp số cộng có số hạng đầu tiên là 50 và hiệu chung là -10. Tìm số hạng thứ 15.

Phần thưởng:

• Sử dụng công thức số hạng thứ n:

  a15 = 50 + (15 – 1)(-10)

• Thay các giá trị ta được:

  a15 = 50 + 14(-10)

• Tính số hạng thứ 15:

  a15 = 50 – 140

• Số hạng thứ 15 là -90.

Ví dụ 3: Đuôi cộng

Cho một cấp số cộng có số hạng đầu tiên là 2, hiệu chung là 3 và một cấp số cộng có số hạng đầu tiên là 5, hiệu chung là 2. Tìm tổng của hai cấp số cộng này.

Phần thưởng:

Kết luận

Cấp số cộng là một công cụ toán học mạnh mẽ được sử dụng trong nhiều lĩnh vực. Bằng cách sử dụng các công thức và khái niệm được trình bày trong bài viết này, chúng ta có thể giải các bài toán liên quan đến dãy số, mô hình hóa hiện tượng tăng hoặc giảm, tìm tổng của nhiều cấp số cộng. và thậm chí tính toán vi phân của một hàm. Sự hiểu biết về cấp số cộng là điều cần thiết cho cả sinh viên và các chuyên gia trong nhiều lĩnh vực khác nhau.

Nếu có thắc mắc vui lòng gửi về số HOTLINE 09633458xxx hoặc địa chỉ email tuyengiaothudo.vn@gmail.com để được giải đáp. Trân trọng!