7 Hằng đẳng thức đáng nhớ

Trong toán học, đẳng thức là một biểu thức đại số luôn đúng với mọi giá trị của một biến. Đẳng thức được sử dụng rộng rãi trong việc giải phương trình, rút ​​gọn biểu thức, giải hệ phương trình,… Dưới đây là 7 hằng số dễ nhớ được sử dụng phổ biến nhất.

H2. Bình phương tổng

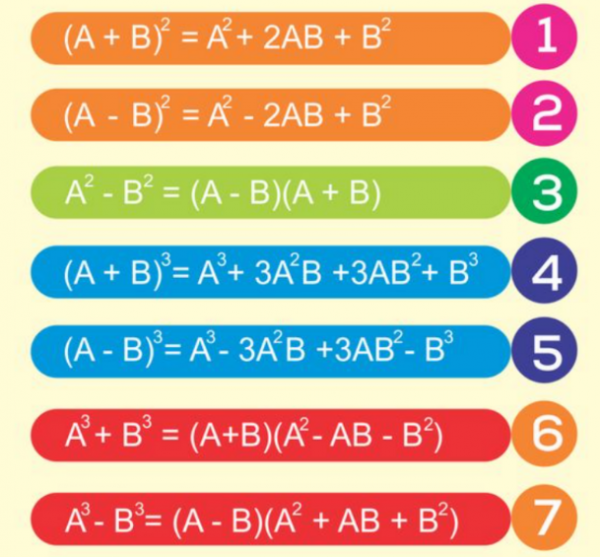
Phương trình hằng số:

(a + b) 2 = a 2 + 2ab + b 2

Ý nghĩa: Bình phương của tổng hai số bằng bình phương của số thứ nhất cộng hai lần tích của hai số đó cộng với bình phương của số thứ hai.

Làm sao để đăng kí:

• Tính bình phương của một tổng.
• Rút gọn biểu thức chứa tổng bình phương.
• Giải phương trình chứa tổng bình phương.

3.1. Ví dụ

• (x + 3) 2 = x 2 + 2(x)(3) + 3 2 = x 2 + 6x + 9
• Rút gọn: (2x – y) 2 = (2x) 2 + 2(2x)(-y) + (-y) 2 = 4x 2 – 4xy + y 2

3.2. Ứng dụng trong giải phương trình

Giải phương trình: x2 + 6x + 9 = 0

• Áp dụng hằng số đẳng thức: (x + 3)² = 0
• Giải phương trình: x + 3 = 0
• Tìm nghiệm: x = -3

H3. Bình phương hiệu ứng

Phương trình hằng số:

(a – b) 2 = a 2 – 2ab + b 2

Ý nghĩa: Bình phương của hiệu hai số bằng bình phương của số thứ nhất trừ hai lần tích của hai số đó cộng với bình phương của số thứ hai.

Làm sao để đăng kí:

• Tính bình phương của sự khác biệt.
• Rút gọn các biểu thức chứa hiệu bình phương.
• Giải các phương trình chứa hiệu bình phương.

3.1. Ví dụ

• (x – 5) 2 = x 2 – 2(x)(5) + 5 2 = x 2 – 10x + 25
• Rút gọn: (3x + 2y) 2 = (3x) 2 – 2(3x)(2y) + (2y) 2 = 9x 2 – 12xy + 4y 2

3.2. Ứng dụng trong giải hệ phương trình

Giải hệ phương trình:

x2 – y2 = 1 x + y = 5

• Bình phương cả hai vế của phương trình thứ hai: (x + y)² = 25
• Áp dụng hằng số đẳng thức: x 2 – y 2 = (x + y)(x – y)
• Thay thế vào phương trình đầu tiên: (x + y)(x – y) = 1
• Giải hệ phương trình:

H4. Sự khác biệt của hai hình vuông

Phương trình hằng số:

a2 – b2 = (a + b)(a – b)

Ý nghĩa: Hiệu của hai bình phương bằng tích của tổng hai số và hiệu của hai số đó.

Làm sao để đăng kí:

• Viết hiệu của hai hình vuông dưới dạng tích.
• Phân tích đa thức.
• Giải phương trình chứa hiệu của hai bình phương.

4.1. Ví dụ

• x² – 9 = (x + 3)(x – 3)
• Phân tích: x⁴ – 16 = (x² + 4)(x² – 4)

4.2. Ứng dụng trong giải hệ phương trình

Giải hệ phương trình:

x2 – y2 = 4 x + y = 6

• Áp dụng đẳng thức: x 2 – y 2 = (x + y)(x – y)
• Thay thế vào phương trình đầu tiên: (x + y)(x – y) = 4
• Giải hệ phương trình:

H5. Tổng của hai khối

Phương trình hằng số:

a³ + b³ = (a + b)(a2 – ab + b2)

Ý nghĩa: Tổng của hai lập phương bằng tích của tổng hai số cộng với hiệu lập phương của hai số cộng với lập phương của tổng hai số.

Làm sao để đăng kí:

• Viết tổng của hai lập phương dưới dạng tích.
• Phân tích đa thức.
• Giải các phương trình chứa tổng của hai lập phương.

5.1. Ví dụ

• x³ + 8 = (x + 2)(x² – 2x + 4)
• Phân tích: 8x³ + y³ = (2x + y)(4x² – 2xy + y²)

5.2. Ứng dụng trong việc tìm giải pháp

Tìm nghiệm của phương trình: x³ + 125 = 0

• Áp dụng phương trình: x³ + 125 = (x + 5)(x² – 5x + 25)
• Giải phương trình:
  • x + 5 = 0 hoặc x² – 5x + 25 = 0
  • Tìm nghiệm: x = -5, x = (5 ± 5i√3) / 2

H6. Sự khác biệt của hai khối

Phương trình hằng số:

a³ – b³ = (a – b)(a2 + ab + b2)

Ý nghĩa: Hiệu của hai lập phương bằng tích của hiệu hai số cộng với tổng lập phương của hai số trừ lập phương của hiệu hai số đó.

Làm sao để đăng kí:

• Viết hiệu của hai hình lập phương dưới dạng tích.
• Phân tích đa thức.
• Giải các phương trình chứa hiệu của hai lập phương.

6.1. Ví dụ

• x³ – 64 = (x – 4)(x² + 4x + 16)
• Phân tích: y³ – 27x³ = (y – 3x)(y² + 3xy + 9x²)

6.2. Ứng dụng trong việc đơn giản hóa biểu thức

Rút gọn biểu thức: (x – 1)(x² + x + 1) – (x³ – 1)

H7. Khối tổng

Phương trình hằng số:

(a + b)³ = a³ + 3a2b + 3ab2 + b³

Ý nghĩa: Lập phương của tổng hai số bằng lập phương của số thứ nhất cộng ba lần tích bình phương của số thứ nhất với số thứ hai cộng ba lần tích của số thứ nhất với bình phương của số thứ hai số đó cộng với lập phương của số thứ hai.

Làm sao để đăng kí:

• Tính lập phương của một tổng.
• Phân tích đa thức.
• Giải các phương trình chứa hình khối.

7.1. Ví dụ

• (x + 2)³ = x³ + 3(x²)(2) + 3(x)(2²) + 2³ = x³ + 6x² + 12x + 8
• Phân tích: 27x³ + 8y³ = (3x + 2y)(9x² – 6xy + 4y²)

7.2. Ứng dụng trong phân tích nhân tử đa thức

Phân tích nhân tử: x³ + 3x²y + 3xy² + y³

Kết luận

• Bảy phương trình đáng nhớ là công cụ hữu ích trong việc giải các bài toán.
• Việc nắm vững và sử dụng linh hoạt các phương trình này sẽ giúp bạn giải được nhiều bài toán một cách chính xác và hiệu quả.
• Luyện tập thường xuyên là cách tốt nhất để ghi nhớ và áp dụng thành thạo các phương trình.

Mọi thắc mắc xin vui lòng gửi về sốHotline 09633458xxx hoặc địa chỉ email. [email protected] để được trả lời. Trân trọng!