3 điểm thẳng hàng là gì? Phương pháp chứng minh 3 điểm thẳng hàng

Trong hình học, khái niệm “3 điểm thẳng hàng” là một trong những khái niệm cơ bản và quan trọng. Nó được sử dụng rộng rãi trong nhiều lĩnh vực, từ toán học, vật lý đến kỹ thuật. Tuy nhiên, không phải ai cũng hiểu rõ khái niệm này và cách chứng minh nó. Trong bài viết này, chúng ta sẽ đi sâu vào khái niệm “3 điểm thẳng hàng”, bao gồm định nghĩa, đặc điểm, phương pháp chứng minh và ứng dụng của nó.

Thế nào là 3 điểm thẳng hàng?

Trong hình học, ba điểm được gọi là “thẳng hàng” nếu chúng nằm trên cùng một đường thẳng. Đây là một khái niệm cơ bản và quan trọng, được sử dụng rộng rãi trong nhiều lĩnh vực như toán học, vật lý, kỹ thuật, v.v.

Để chứng minh ba điểm thẳng hàng, ta có thể sử dụng hai phương pháp chính:

Phương pháp chứng minh 3 điểm thẳng hàng bằng tích vô hướng

Phương pháp này dựa trên tính chất của tích vô hướng. Tích vô hướng của hai vectơ bằng 0 khi và chỉ khi hai vectơ song song. Do đó, nếu chúng ta xét 3 điểm A, B, C và tính tích vô hướng của các vectơ AB và AC, nếu tích này bằng 0 thì 3 điểm A, B, C sẽ thẳng hàng.

Phương pháp chứng minh 3 điểm thẳng hàng bằng vectơ pháp tuyến

Phương pháp này dựa trên tính chất của vectơ pháp tuyến. Vectơ pháp tuyến của hai vectơ bằng 0 khi và chỉ khi hai vectơ song song. Do đó, nếu chúng ta xét 3 điểm A, B, C và tính vectơ pháp tuyến của các vectơ AB và AC, nếu vectơ pháp tuyến này bằng 0 thì 3 điểm A, B, C sẽ thẳng hàng.

Phương pháp chứng minh 3 điểm thẳng hàng bằng tích vô hướng

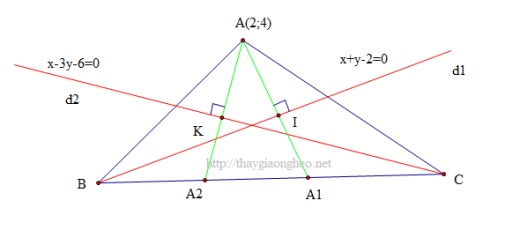
Như đã nói ở trên, phương pháp chứng minh 3 điểm thẳng hàng bằng tích vô hướng dựa trên tính chất của tích vô hướng. Cụ thể như sau:

Tính chất của tích vô hướng

Tích vô hướng của hai vectơ a và b, ký hiệu là a · b, được định nghĩa như sau:

a · b = |a||b|cos(θ)

Trong đó:

• |a| và |b| là độ dài (hoặc độ lớn) của vectơ a và b.
• θ là góc giữa hai vectơ a và b.

Các tính chất quan trọng của tích vô hướng là:

a · b = 0 khi và chỉ khi a và b song song

Chứng minh rằng ba điểm thẳng hàng theo tích vô hướng

Giả sử ta có 3 điểm A, B, C. Để chứng minh 3 điểm này thẳng hàng, ta có thể làm như sau:

1. Tính các vectơ AB và AC.
2. Tính tích vô hướng của AB và AC.
3. Nếu tích vô hướng AB · AC = 0 thì ba điểm A, B, C thẳng hàng.

Cụ thể, chúng ta có:

• AB = B – A
• AC = C – A
• AB · AC = (B – A) · (C – A) = 0

Vì tích vô hướng AB · AC = 0 nên theo tính chất của tích vô hướng, các vectơ AB và AC phải song song, nghĩa là 3 điểm A, B, C thẳng hàng.

Như vậy, phương pháp chứng minh 3 điểm thẳng hàng bằng tích vô hướng là một cách tiếp cận hiệu quả và thường được sử dụng trong nhiều bài toán hình học.

Phương pháp chứng minh 3 điểm thẳng hàng bằng vectơ pháp tuyến

Bên cạnh phương pháp chứng minh bằng tích vô hướng, chúng ta cũng có thể sử dụng phương pháp chứng minh bằng vectơ pháp tuyến. Cách tiếp cận này cũng dựa trên các tính chất của vectơ pháp tuyến.

Tính chất của vectơ pháp tuyến

Vectơ pháp tuyến của hai vectơ a và b, ký hiệu là a × b, được định nghĩa như sau:

a × b = (|a||b|sin(θ))n

Trong đó:

• |a| và |b| là độ dài (hoặc độ lớn) của vectơ a và b.
• θ là góc giữa hai vectơ a và b.
• n là vectơ pháp tuyến, có độ dài |a × b| và hướng vuông góc với a và b.

Các tính chất quan trọng của vectơ pháp tuyến là:

a × b = 0 khi và chỉ khi a và b song song

Chứng minh rằng 3 điểm thẳng hàng sử dụng vectơ pháp tuyến

Giả sử ta có 3 điểm A, B, C. Để chứng minh 3 điểm này thẳng hàng, ta có thể làm như sau:

1. Tính các vectơ AB và AC.
2. Tính các vectơ pháp tuyến của AB và AC.
3. Nếu vectơ pháp tuyến AB × AC = 0 thì ba điểm A, B, C thẳng hàng.

Cụ thể, chúng ta có:

• AB = B – A
• AC = C – A
• AB × AC = (B – A) × (C – A) = 0

Vì vectơ pháp tuyến AB × AC = 0 nên theo tính chất của vectơ pháp tuyến, vectơ AB và AC phải song song, nghĩa là 3 điểm A, B, C thẳng hàng.

Như vậy, phương pháp chứng minh 3 điểm thẳng hàng bằng vectơ pháp tuyến cũng là một cách tiếp cận hiệu quả và thường được sử dụng trong nhiều bài toán hình học.

Định nghĩa 3 điểm thẳng hàng

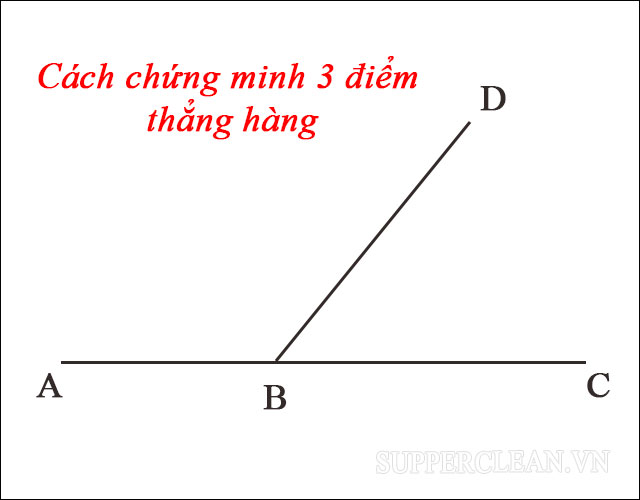
Định nghĩa chính thức của “3 điểm trên một đường thẳng” là:

Ba điểm A, B, C được gọi là “thẳng hàng” nếu chúng nằm trên cùng một đường thẳng.

Nói cách khác, 3 điểm A, B, C được gọi là thẳng hàng nếu tồn tại một đường thẳng l đi qua cả 3 điểm này.

Đặc điểm của 3 điểm thẳng hàng

Đặc điểm của 3 điểm thẳng hàng là:

1. Tích vô hướng là 0

Như đã trình bày ở trên, nếu ba điểm A, B, C thẳng hàng thì tích vô hướng của các vectơ AB và AC bằng 0.

2. Vectơ pháp tuyến là 0

Tương tự, nếu ba điểm A, B, C thẳng hàng thì vectơ pháp tuyến của vectơ AB và AC bằng 0.

3. Trên cùng một dòng

Định nghĩa về 3 điểm thẳng hàng là 3 điểm này nằm trên cùng một đường thẳng.

4. Có thể xác định được bằng 2 điểm

Nếu ta biết hai điểm A và B thẳng hàng thì ta có thể xác định được điểm C nằm trên đường thẳng đi qua A và B.

5. Trong một mặt phẳng không có 3 điểm thẳng hàng.

Trong một mặt phẳng, không thể có nhiều hơn 2 điểm thẳng hàng. Vì nếu có 3 điểm thẳng hàng, chúng sẽ xác định một đường thẳng, không nằm hoàn toàn trong mặt phẳng.

Ứng dụng của 3 điểm thẳng hàng trong hình học và vật lý

Khái niệm ba điểm thẳng hàng có nhiều ứng dụng quan trọng trong hình học và vật lý, bao gồm:

1. Xác định đường thẳng

Biết 3 điểm thẳng hàng, ta có thể xác định được đường thẳng duy nhất đi qua cả 3 điểm đó.

2. Tính độ dài và góc

Từ 3 điểm thẳng hàng, ta có thể tính được độ dài các đoạn thẳng, góc giữa các vectơ, v.v.

3. Phương trình đường thẳng

Biết ba điểm thẳng hàng, ta có thể viết phương trình đường thẳng đi qua chúng dưới dạng phương trình tham số hoặc phương trình điểm-vectơ.

4. Vật lý: Chuyển động thẳng

Trong vật lý, khi một vật chuyển động theo đường thẳng, vị trí của vật tại 3 thời điểm khác nhau sẽ nằm trên một đường thẳng.

5. Vật lý: Chùm sáng, chùm tia laser

Trong quang học, tia sáng và chùm tia laser thường được coi là đường thẳng. Để xác định đường đi của chúng, chúng ta cần xác định 3 điểm thẳng hàng trên tia.

Như vậy, khái niệm 3 điểm thẳng hàng rất quan trọng và có nhiều ứng dụng thực tế trong các lĩnh vực như toán học, vật lý, kỹ thuật, v.v.

Bài toán chứng minh 3 điểm thẳng hàng

Trong các bài toán hình học, chứng minh ba điểm thẳng hàng là yêu cầu chung. Có nhiều cách tiếp cận khác nhau để chứng minh điều này, tùy thuộc vào dữ liệu và yêu cầu của bài toán.

Một số phương pháp phổ biến để chứng minh ba điểm thẳng hàng bao gồm:

1. Sử dụng tích vô hướng

Như hình trên, nếu tích vô hướng của 2 vectơ AB và AC bằng 0 thì 3 điểm A, B, C thẳng hàng.

2. Sử dụng vectơ pháp tuyến

Tương tự, nếu vectơ pháp tuyến của 2 vectơ AB và AC bằng 0 thì 3 điểm A, B, C thẳng hàng.

3. Sử dụng phương trình đường thẳng

Nếu ba điểm A, B, C cùng thỏa mãn phương trình đường thẳng thì chúng thẳng hàng.

4. Tỷ lệ sử dụng

Nếu tỉ số các đoạn thẳng AB, BC, AC bằng nhau thì ba điểm A, B, C thẳng hàng.

5. Sử dụng tính chất đối xứng

Nếu ba điểm A, B, C thỏa mãn một số tính chất đối xứng nào đó thì chúng thẳng hàng.

Trong các bài toán thực tế, người giải thường phải vận dụng linh hoạt các phương pháp trên để chứng minh ba điểm thẳng hàng dựa vào dữ kiện và yêu cầu của bài toán.

Bài tập liên quan đến 3 điểm thẳng hàng

Các bài tập liên quan đến 3 điểm thẳng hàng bao gồm:

1. Chứng minh rằng 3 điểm thẳng hàng

Cho 3 điểm, hãy chứng minh chúng thẳng hàng bằng các phương pháp nêu trên.

2. Tính độ dài

Cho 3 điểm trên một đường thẳng, tính độ dài các đoạn thẳng AB, BC, AC.

3. Xác định phương trình của đường thẳng

Cho ba điểm thẳng hàng, hãy xác định phương trình đường thẳng đi qua chúng.

4. Ứng dụng vào vật lý

Cho ví dụ về chuyển động thẳng của một vật, cần xác định 3 vị trí thẳng hàng của vật tại các thời điểm khác nhau.

5. Vấn đề kinh tế

Áp dụng khái niệm 3 điểm thẳng hàng vào bài toán tối ưu hóa trong kinh tế, với điều kiện các ràng buộc tạo thành 3 điểm thẳng hàng.

Các loại bài tập này giúp học sinh rèn luyện tư duy logic, tính toán và vận dụng kiến ​​thức vào thực tiễn.

Tổng quát hóa khái niệm 3 điểm thẳng hàng vào không gian đa chiều

Trong không gian đa chiều, khái niệm ba điểm thẳng hàng vẫn được áp dụng tương tự như trong không gian hai chiều. Tuy nhiên, để chứng minh ba điểm thẳng hàng trong không gian ba chiều trở lên, chúng ta cần sử dụng các phép toán vectơ phức tạp hơn và đại số tuyến tính.

Một khái quát của khái niệm này là: Ba điểm A, B, C trong không gian đa chiều được gọi là thẳng hàng nếu tồn tại một vectơ v sao cho các vectơ AB và AC, phân biệt v, cùng nằm trên một mặt phẳng vuông góc với v.

Việc tổng quát hóa khái niệm 3 điểm thẳng hàng thành không gian nhiều chiều hơn mở rộng ứng dụng của nó sang các lĩnh vực như đại số tuyến tính, hình học không gian, học máy, v.v.

Thảo luận và mở rộng

Khái niệm 3 điểm thẳng hàng là một trong những khái niệm cơ bản và quan trọng trong hình học Euclid. Việc hiểu và vận dụng linh hoạt khái niệm này không chỉ giúp chúng ta giải quyết các bài toán hình học mà còn mở ra nhiều cơ hội ứng dụng trong các lĩnh vực khác như vật lý, kỹ thuật, kinh tế, v.v.

Thông qua việc trình bày, tính toán và ứng dụng 3 điểm thẳng hàng, chúng ta có thể rèn luyện kỹ năng tư duy logic, logic học và phát triển khả năng giải quyết vấn đề.

Kết luận

Trong bài viết này, chúng ta đã tìm hiểu về khái niệm 3 điểm thẳng hàng, phương pháp chứng minh, đặc điểm, ứng dụng và các bài tập liên quan. Việc hiểu được khái niệm này không chỉ giúp chúng ta nắm vững kiến ​​thức hình học mà còn mở ra nhiều cơ hội trong việc ứng dụng nó vào thực tế và các lĩnh vực khác. Hy vọng bài viết này sẽ giúp bạn hiểu rõ hơn về 3 điểm thẳng hàng và vận dụng linh hoạt vào giải toán.

Mọi thắc mắc vui lòng gửi về Hotline 09633458xxx hoặc địa chỉ email [email protected] để làm rõ. Trân trọng!